
동적계획법(DP)은 메모리를 적절히 사용하여 수행 시간 효율성을 향상시키는 기법이다. 이미 계산된 결과는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 하여 시간복잡도를 획기적으로 줄일 수 있다.
DP 문제 조건
- 최적 부분 구조 (Optimal Substructure)
큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아 큰 문제를 해결할 수 있는 경우 - 중복되는 부분 문제 (Overlapping Subproblem)
동일한 작은 문제를 반복적으로 호출하여 해결해야 할 경우
2748번: 피보나치 수 2
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
피보나치 수열
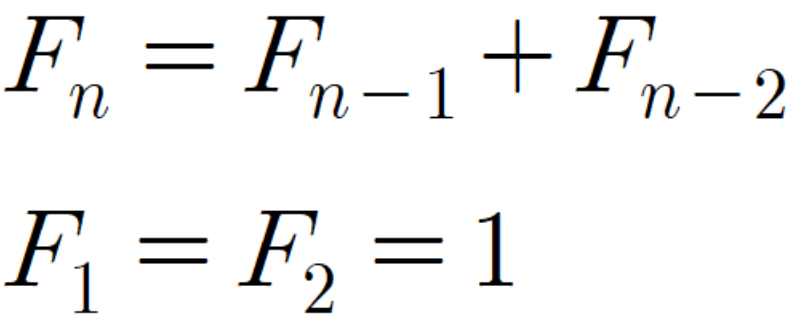
피보나치 수열을 단순 재귀로 구현하면 다음과 같다.
public static int fibo(int x) {
if( x==1 || x==2 ) return 1;
return fibo(x - 1) + fibo(x - 2);
}
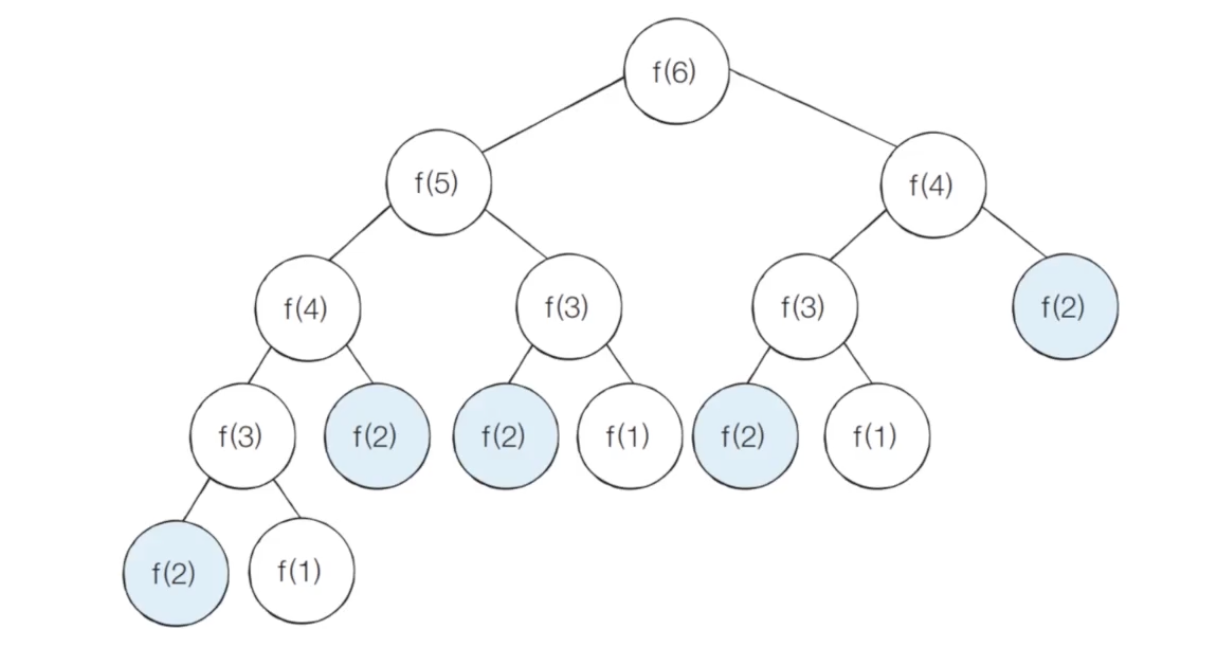
단순 재귀 함수로 피보나치 수열을 해결하면 지수 시간 복잡도를 가지며 다음과 같이 f(2)가 여러 번 호출되는 것을 확인할 수 있다.
➜ 중복되는 부분 문제
메모이제이션은 다이나믹 프로그래밍을 구현하는 방법 중 하나로 메모이제이션을 통해 피보나치 수열을 해결하면 시간 복잡도는 O(N)이 된다.
static int[] dp; // 피보나치 수열 값을 저장할 배열 선언
public int fibo(int n) {
if(dp[n] > 0 ) return dp[n]; // 메모이제이션 ✨
if (n < 2) return dp[n] = n;
else
return dp[n] = fibo(n - 1) + fibo(n - 2);
}
DP vs 분할정복
DP와 분할정복은 모두 최적 부분 구조를 가질 때 사용할 수 있다. 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아 큰 문제를 해결할 수 있는 상황에 사용한다.
DP와 분할정복의 차이점은 부분 문제의 중복이다. 분할정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않는다.
DP 문제에 접근하는 법
일단 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤 작은 문제에서 구한 답이 큰 문제에서 그대로 사용되는 경우, 메모이제이션을 이용하여 코드를 개선할 수 있다.
💡 DFS로 구현했을 때, 시간초과가 난 경우 ➜ DP
[JAVA/알고리즘] 메모이제이션(Memoization) 개념과 예제
메모이제이션(Memoization) 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행속도를 빠르게 하는
gangintheremark.tistory.com
'Algorithm > 알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘 : 하나의 출발점에서 다른 모든 출발지까지 최단 경로 계산 (0) | 2024.03.03 |
|---|---|
| [이코테] 다양한 동적 계획법(DP) 문제 풀이 - JAVA 자바 (0) | 2024.02.17 |
| [JAVA] 바이너리 인덱스 트리 (Binary Indexed Tree, BIT) (0) | 2023.11.16 |
| [JAVA] 우선순위 큐 (PriorityQueue) (1) | 2023.10.16 |
| [JAVA/자료구조] 스택(Stack)과 큐(Queue) (0) | 2023.10.16 |

