바이너리 인덱스 트리(Binary Indexed Tree, BIT)는 2진법 인덱스 구조를 활용해 구간 합 문제를 해결해 줄 수 있는 자료구조이다. 펜윅 트리(fenwick tree)라고도 한다.
바이너리 인덱스 트리를 구현하려면, 어떤 수 X를 이진수로 나타냈을 때, 0이 아닌 마지막 비트를 알아야한다.
0이 아닌 마지막 비트를 찾는 방법
어떤 수 X의 0이 아닌 마지막 비트를 찾기 위해서 X & -X를 계산하면 된다.
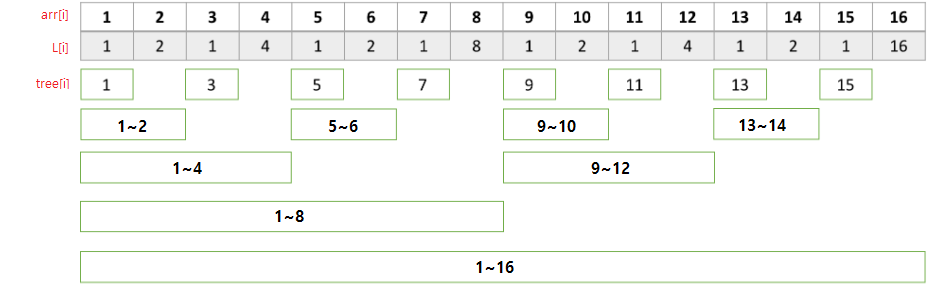
L[i]는 i를 2진수로 나타냈을 때, 0이 아닌 마지막 비트값을 저장하고 있는 배열이다.
즉, 3을 이진수로 나타냈을 때 011 이므로 0이 아닌 가장 마지막 비트값은 L[3]=1 이다.
Tree[i]는 arr[i]로부터 앞으로 L[i] 개의 합을 저장하고 있는 배열이다.
- Tree[1]는 arr[1]로부터 앞으로 L[1] 개의 합 ➜ 1개의 합
- Tree[2]는 arr[2]로부터 앞으로 L[2] 개의 합 ➜ 2개의 합
...
- Tree[4]는 arr[4]로부터 앞으로 L[4] 개의 합 ➜ 4개의 합
...
- Tree[8]는 arr[8]로부터 앞으로 L[8] 개의 합 ➜ 8개의 합
변경 (Update)
0이 아닌 마지막 비트만큼 더하면서 구간들의 값을 변경
어떤 수를 변경한 경우에는 자신이 영향을 끼치는 부분 또한 바꿔줘야 한다. arr[3]을 변경한다면 아래 노란색 부분들을 update해주면 된다.
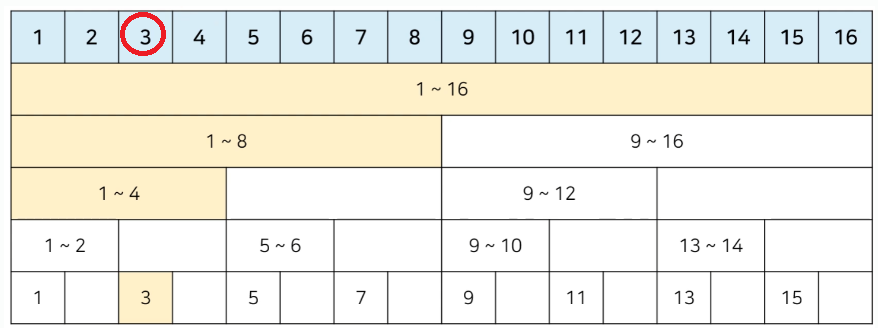
이를 코드로 나타내면 다음과 같다. 시간복잡도는 O(logN) 이다.
원래 있던 수를 변경하려면 원래 있던 수와 변경하려는 수의 차이diff 만큼을 update 하면 된다.
void update(int i, int diff) {
while(i<=n) {
tree[i] += diff;
i += (i & -i);
}
}
누적합 구하기 (Prefix Sum)
0이 아닌 마지막 비트만큼 빼면서 구간들의 값의 합 계산
arr[11]까지의 누적합을 구한다면 아래 노란색 부분들의 값을 더해주면 된다.
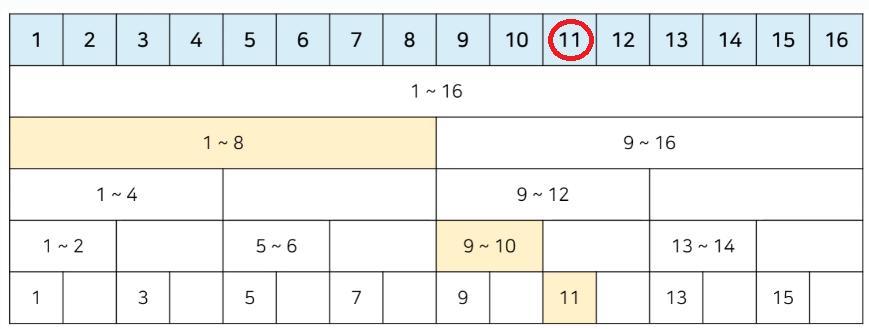
이를 코드로 나타내면 다음과 같다. 시간복잡도는 O(logN) 이다.
int prefix_sum(int i) {
int result = 0;
while(i > 0) {
result += tree[i];
i -= (i & -i);
}
}
시간복잡도는 O(logN) 이다.
[BOJ] 2042 - 구간 합 구하기
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Solution {
static long[] arr;
static long[] tree;
static int n, m, k;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
arr = new long[n + 1];
tree = new long[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = Long.parseLong(br.readLine());
update(i, arr[i]);
}
for (int i = 0; i < m + k; i++) {
st = new StringTokenizer(br.readLine().trim());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
if (a == 1) {
long diff = c - arr[b];
arr[b] = c;
update(b, diff);
} else {
System.out.println(sum((int) c) - sum(b - 1));
}
}
}
public static void update(int i, long diff) {
while (i <= n) {
tree[i] += diff;
i += (i & -i);
}
}
public static long sum(int i) {
long result = 0;
while (i > 0) {
result += tree[i];
i -= (i & -i);
}
return result;
}
}
'Algorithm > 알고리즘' 카테고리의 다른 글
| [이코테] 다양한 동적 계획법(DP) 문제 풀이 - JAVA 자바 (0) | 2024.02.17 |
|---|---|
| [JAVA/알고리즘] 동적계획법 (DP, Dynamic Programming) (0) | 2024.02.13 |
| [JAVA] 우선순위 큐 (PriorityQueue) (1) | 2023.10.16 |
| [JAVA/자료구조] 스택(Stack)과 큐(Queue) (0) | 2023.10.16 |
| [JAVA] 이진트리 순회(DFS, BFS) (0) | 2023.09.17 |
바이너리 인덱스 트리(Binary Indexed Tree, BIT)는 2진법 인덱스 구조를 활용해 구간 합 문제를 해결해 줄 수 있는 자료구조이다. 펜윅 트리(fenwick tree)라고도 한다.
바이너리 인덱스 트리를 구현하려면, 어떤 수 X를 이진수로 나타냈을 때, 0이 아닌 마지막 비트를 알아야한다.
0이 아닌 마지막 비트를 찾는 방법
어떤 수 X의 0이 아닌 마지막 비트를 찾기 위해서 X & -X를 계산하면 된다.

L[i]는 i를 2진수로 나타냈을 때, 0이 아닌 마지막 비트값을 저장하고 있는 배열이다.
즉, 3을 이진수로 나타냈을 때 011 이므로 0이 아닌 가장 마지막 비트값은 L[3]=1 이다.
Tree[i]는 arr[i]로부터 앞으로 L[i] 개의 합을 저장하고 있는 배열이다.
- Tree[1]는 arr[1]로부터 앞으로 L[1] 개의 합 ➜ 1개의 합
- Tree[2]는 arr[2]로부터 앞으로 L[2] 개의 합 ➜ 2개의 합
...
- Tree[4]는 arr[4]로부터 앞으로 L[4] 개의 합 ➜ 4개의 합
...
- Tree[8]는 arr[8]로부터 앞으로 L[8] 개의 합 ➜ 8개의 합
변경 (Update)
0이 아닌 마지막 비트만큼 더하면서 구간들의 값을 변경
어떤 수를 변경한 경우에는 자신이 영향을 끼치는 부분 또한 바꿔줘야 한다. arr[3]을 변경한다면 아래 노란색 부분들을 update해주면 된다.

이를 코드로 나타내면 다음과 같다. 시간복잡도는 O(logN) 이다.
원래 있던 수를 변경하려면 원래 있던 수와 변경하려는 수의 차이diff 만큼을 update 하면 된다.
void update(int i, int diff) {
while(i<=n) {
tree[i] += diff;
i += (i & -i);
}
}
누적합 구하기 (Prefix Sum)
0이 아닌 마지막 비트만큼 빼면서 구간들의 값의 합 계산
arr[11]까지의 누적합을 구한다면 아래 노란색 부분들의 값을 더해주면 된다.

이를 코드로 나타내면 다음과 같다. 시간복잡도는 O(logN) 이다.
int prefix_sum(int i) {
int result = 0;
while(i > 0) {
result += tree[i];
i -= (i & -i);
}
}
시간복잡도는 O(logN) 이다.
[BOJ] 2042 - 구간 합 구하기
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Solution {
static long[] arr;
static long[] tree;
static int n, m, k;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
arr = new long[n + 1];
tree = new long[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = Long.parseLong(br.readLine());
update(i, arr[i]);
}
for (int i = 0; i < m + k; i++) {
st = new StringTokenizer(br.readLine().trim());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
if (a == 1) {
long diff = c - arr[b];
arr[b] = c;
update(b, diff);
} else {
System.out.println(sum((int) c) - sum(b - 1));
}
}
}
public static void update(int i, long diff) {
while (i <= n) {
tree[i] += diff;
i += (i & -i);
}
}
public static long sum(int i) {
long result = 0;
while (i > 0) {
result += tree[i];
i -= (i & -i);
}
return result;
}
}
'Algorithm > 알고리즘' 카테고리의 다른 글
| [이코테] 다양한 동적 계획법(DP) 문제 풀이 - JAVA 자바 (0) | 2024.02.17 |
|---|---|
| [JAVA/알고리즘] 동적계획법 (DP, Dynamic Programming) (0) | 2024.02.13 |
| [JAVA] 우선순위 큐 (PriorityQueue) (1) | 2023.10.16 |
| [JAVA/자료구조] 스택(Stack)과 큐(Queue) (0) | 2023.10.16 |
| [JAVA] 이진트리 순회(DFS, BFS) (0) | 2023.09.17 |

