[BOJ] 12865. 평범한 배낭 - JAVA 자바 ✨냅색 알고리즘✨

12865번: 평범한 배낭

냅색 알고리즘

이 문제는 DP를 대표하는 배낭 문제로 냅색 알고리즘(knapsack)로 풀이하는 문제이다. 배낭이 수용할 수 있는 최대 무게가 정해지고 배낭에 넣은 물건들의 가치의 최대합을 구하는 문제이다.

 

냅색 알고리즘은 짐을 쪼갤 수 있는 경우와 짐을 쪼갤 수 없는 경우로 나눌 수 있다.

• Fraction Knapsack : 짐을 쪼갤 수 있는 배낭문제로 탐욕 알고리즘(greedy)로 풀이
• 0/1 Knapsack : 짐을 쪼갤 수 없는 배낭문제로 동적계획법(DP)로 풀이

이 문제는 짐을 쪼갤 수 없기 때문에 동적계획법(DP)으로 해결해야한다.

---

이 문제의 핵심은 무게 w에 넣을 수 있는 물건의 최대가치를 저장하는 것이다.

 

무게 W[] 배열과 가치 V[] 배열이 있다고 할 때, 예제로는 다음과 같다.
(W, V) = (6, 13), (4, 8), (3, 6), (5, 12), 배낭이 수용 가능한 최대 무게 K = 7 이다.

dp[물건index][w] = 수용 가능한 최대 무게가 w일 때, 물건의 최대가치

 

먼저 dp[0], dp[1], dp[2]는 수용 가능한 물건이 없으므로 모두 0이다.

 

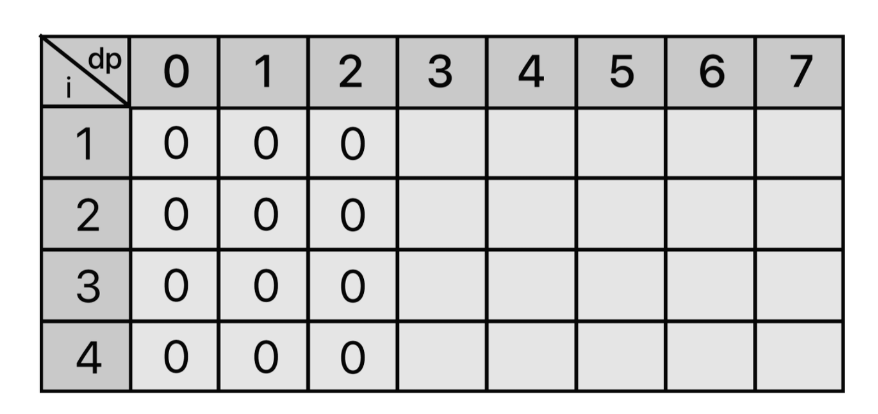
수용 가능한 무게가 3일 때, 3번째 물건인 (3,6)을 넣을 수 있으므로 dp[3][3] = 6이 된다. i=4 일 때는 4번째 물건을 넣을 수 없고, 이전 i=3에 대하여 탐색할 때 채워진 값을 그대로 갖고 있게 되는 것이다 ➜ 누적탐색

 

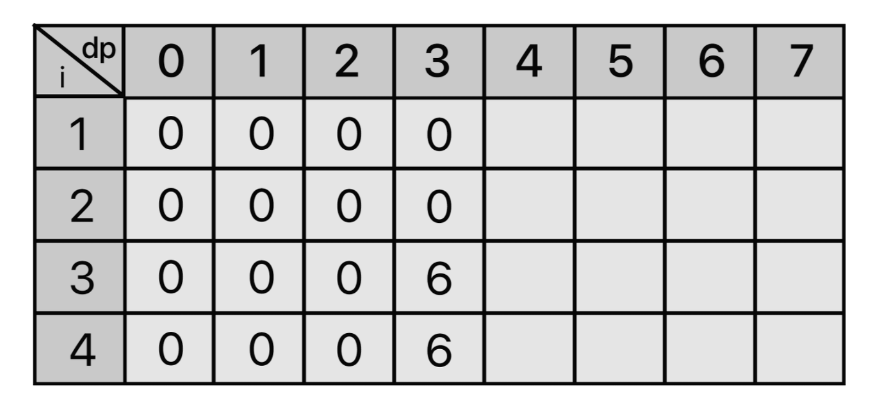
수용 가능한 무게가 4일 때, 2번째 물건인 (4,8)을 넣을 수 있으므로 dp[2][4] = 8이 된다. 여기서 중요한 점은 물건을 탐색하기 전에 i의 이전의 값에 대한 dp에 메모이제이션 되어있는 값을 가져와야한다.

 

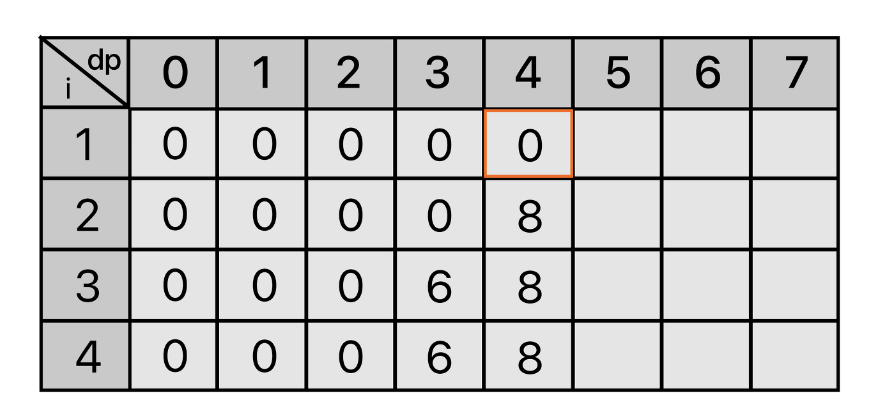
마찬가지로 수용 가능한 무게가 5일 때, i = 1, 2, 3은 이전 i 의 dp값을 갖게될 것이고, 4번째 물건인 (5,12)을 넣을 수 있으므로 dp[4][5] = 12가 된다.

 

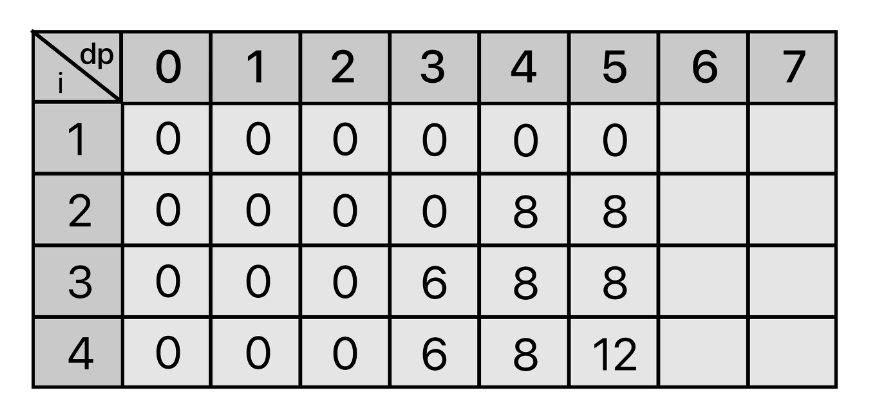
수용 가능한 무게가 7일 때부터는 물건이 두 개 이상의 조합으로 구성할 수 있다.

 

먼저 이전 i의 dp 값(dp[0][7]=0)을 가져온다. 그리고 1번째 물건은 (6,13) 으로 무게가 6인 물건 + 무게가 1인 물건 의 조합을 가질 수 있다. 즉, V[1] + dp[i-1][7-W[1]] 와 이전 무게의 값 dp[0][7] 을 비교하여 더 큰 값을 저장해준다. 13 > 0으로 dp[1][7] = 13이 된다.

 

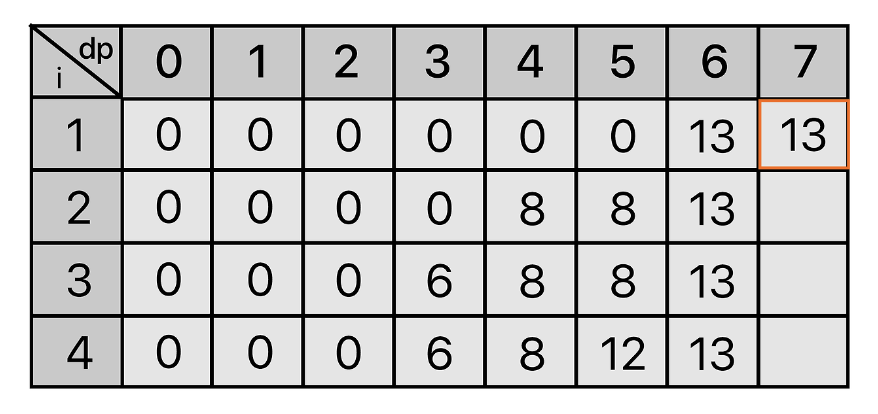
V[3] + dp[i-1][7-W[3]] = 6 + 8 = 14로 이전 무게의 값 dp[2][7] = 13 보다 크므로 dp[3][7] = 14가 저장된다.

 

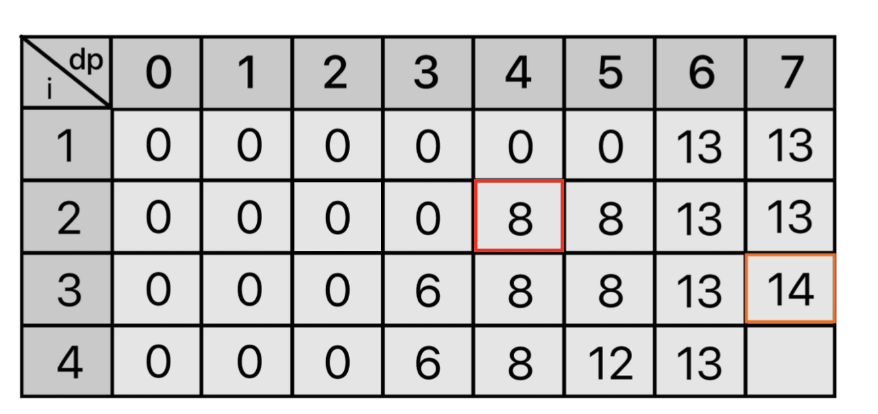
이러한 두 가지 원리를 통해 다음과 같은 점화식을 만들 수 있다.

if(W[i] > K) dp[i][k] = dp[i-1][k]
if(i>0 and W[i] ≤ K) dp[i][k] = max( V[i] + dp[i-1][k-W[i]], dp[i-1][k] )

---

Bottom-Up 방식

하위 인덱스부터 시작하기 때문에 i - 1 로 인해 인덱스 범위 밖을 참조하게 될 수 있어 W, V은 각각 N+1 사이즈로 선언해준다.

public class Main {
    private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    private static StringTokenizer st;

    public static void main(String[] args) throws IOException {
        st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int K = Integer.parseInt(st.nextToken());
        int[] W = new int[N + 1];
        int[] V = new int[N + 1];
        int[][] dp = new int[N + 1][K + 1];
        for (int i = 1; i <= N; i++) {
            st = new StringTokenizer(br.readLine());
            W[i] = Integer.parseInt(st.nextToken());
            V[i] = Integer.parseInt(st.nextToken());
        }

        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= K; j++) {
                if (W[i] > j) 
                    dp[i][j] = dp[i - 1][j];
                else
                    dp[i][j] = Math.max(dp[i - 1][j], V[i] + dp[i - 1][j - W[i]]);
            }
        }
        System.out.println(dp[N][K]);
    }
}

 

Top-Down 방식

재귀를 이용하여 탐색해주는 방식이다.

public class Main {
    static int N, K;
    static int[] W;
    static int[] V;
    static Integer[][] dp;

    public int knapsack(int i, int k) {
        if (i < 0)
            return 0;
        if (dp[i][k] == null) {
            if (W[i] > k)
                dp[i][k] = knapsack(i - 1, k); 
            else 
                dp[i][k] = Math.max(knapsack(i - 1, k), knapsack(i - 1, k - W[i]) + V[i]);
        }
        return dp[i][k];
    }

    public static void main(String[] args) throws IOException {
        Main M = new Main();
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        K = Integer.parseInt(st.nextToken());
        dp = new Integer[N][K + 1];

        W = new int[N];
        V = new int[N];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            W[i] = Integer.parseInt(st.nextToken());
            V[i] = Integer.parseInt(st.nextToken());

        }

        System.out.println(M.knapsack(N - 1, K));
    }
}

 

✨ Reference

- https://st-lab.tistory.com/141